Korrelation
Der Korrelationskoeffizient $\rho_{x, y}$ misst für zwei metrische Variablen $x$ und $y$ die Stärke des linearen Zusammenhangs. Der Koeffizient kann zwischen $-1$ (negativer Zusammenhang) und $1$ (positiver Zusammenhang) variieren:

Der Korrelationskoeffizient ist definiert als: $$ \rho_{x, y} = \frac{s_{x, y}^2}{s_xs_y} = \frac{\sum_{i=1}^{N}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^{N}(x_i-\bar{x})^2\sum_{i=1}^{N}(y_i-\bar{y})^2}} $$
Die Ausdrücke im Nenner sind die jeweiligen Standardabweichungen der Reihen. Sie dienen zur Normalisierung der Statistik, sodass diese nur Werte zwischen $-1$ und $1$ annimmt. Beachten Sie, dass in der Formel der Bruch durch $\frac{1}{N-1}$ gekürzt wurde.
Im Zähler steht die empirische Kovarianz definiert als: $$ s_{x, y}^2 = \frac{1}{N-1}\sum_{i=1}^{N}(x_i-\bar{x})(y_i-\bar{y}) $$
Nehmen Sie vereinfachend an, dass $\bar{x} = \bar{y} = 0$. Die Kovarianz ist dann der Mittelwert über die paarweise miteinander multiplizierten Beobachtungen. Sind beide Faktoren positiv oder beide Faktoren negativ, so tragen diese zu einer positiven Kovarianz bei. Haben die Faktoren unterschiedliche Vorzeichen, so tragen diese zu einer negativen Kovarianz bei. Kleine numerische Werte tragen nur wenig zur Kovarianz bei.
Mit pandas können Sie natürlich auch Korrelationen ausrechnen:
import pandas as pd
df = pd.read_csv("../data/Library_Usage.csv")
df['Total Checkouts'].corr(df['Total Renewals'])
Anscombe-Quartett (30 Min)
Das Anscombe Quartett ist ein Datenstatz, der aus 4 bivariaten Verteilungen besteht. Über die Spaltennamen ['x1', 'y1'], ['x2', 'y2'], ..., ['x4', 'y4'] können die zusammengehörenden Datenpaare ausgewählt werden.
- Lesen Sie den Datensatz ein.
- Berechnen Sie den Mittelwert, Median und die Standardabweichung der Spalten.
- Berechnen Sie jeweils die Korrelation zweier zusammenhängender Spalten
[x<i>, y<i>]. - Erstellen Sie jeweils ein Streudiagram zweier zusammenhängender Spalten
[x<i>, y<i>]. - Was fällt Ihnen auf? Informieren Sie sich über den Datensatz hier.
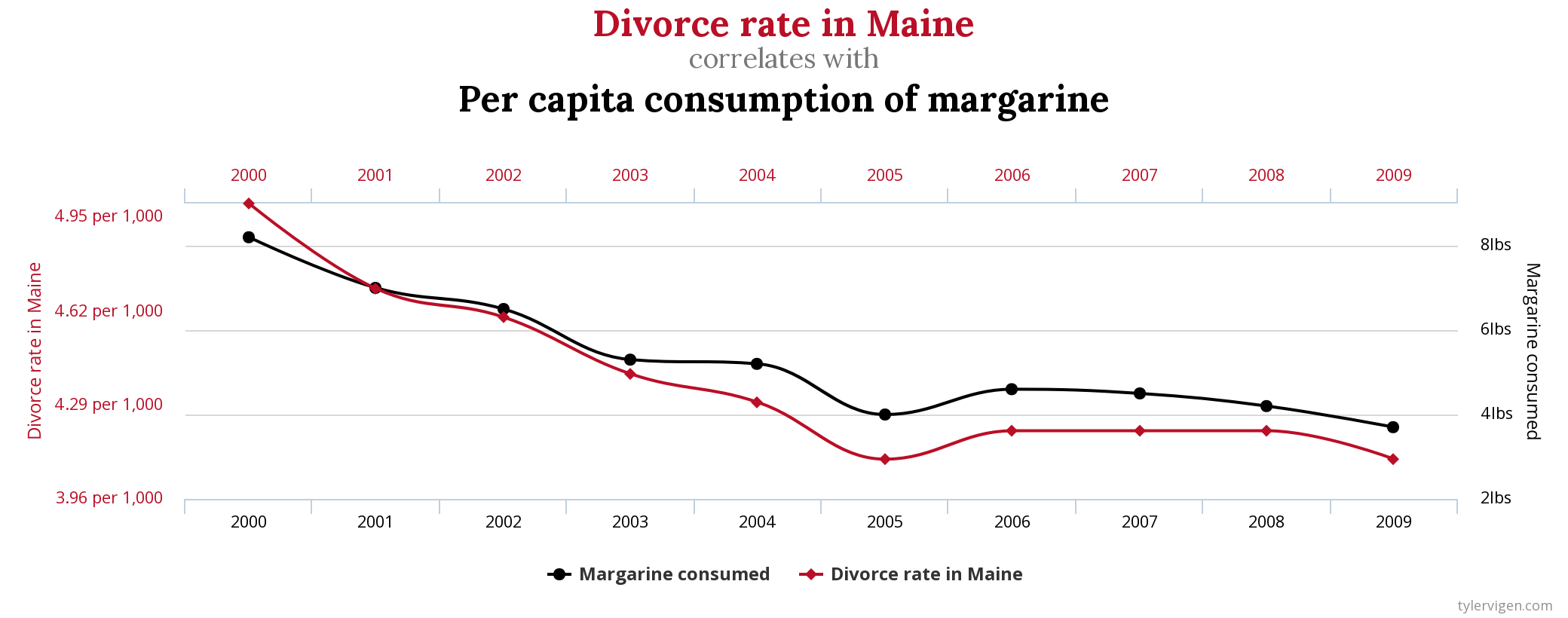
Beispiel für Scheinkorrelation in Zeitreihen ($\rho_{x,y}=0.99$): Große positive oder negative Korrelationen sind kein Indiz für kausale Zusammenhänge! Quelle: tylervigen.com